 LQI
LQI
熱制御(最適レギュレータ)
で扱った制御対象を考えてみます。すでに最適レギュレータのフィードバックゲインは求めてあります。センサー(サーミスタ)特性が非線形なので、実際にはこのままでは使えません。サーミスタのリニアライズは別の手段行うことを前提にします。
計算式はこちらの文献もを参考にしました。
参考文献1のp99~を参考に
x[i+1] = Ax[i]+bu[i]
y[i] = cx[i]
このときの最適1型サーボゲインは
[h,k] = [fA , fB+I ][A-I , B ; C , 0]-1
fは最適レギュレータのフィードバックゲイン
制御則は
u[i] = -hx[i] + kz[i];
z[i+1] = z[i] + (Yr - y[i]);
*************では 計算プログラムです ********************
A B C Fは熱制御(最適レギュレータ)
で求めた値を使います。F=f Fd=h Kd=kです。
A=
0.9997050 0.0975314
-0.0058519 0.9509393
B=
0.0049175
0.0975314
C=
1 0
F=
0.88019 1.20637
Fd Kdは下記の計算で求めものを記載しておきます。
Fd=
17.973 10.598
Kd = 0.94019
*************実際の計算はここから********************
Ad = A
Bd = B
Cd = C
[n m]=size(Bd);
ABC=[Ad-eye(n) Bd;Cd zeros(m)];
FSD=[F*Ad F*Bd+eye(m)]*inv(ABC);
Fd=FSD(:,1:n)
Kd=FSD(:,n+1:m+n)
ft=2;
dt=0.01;
N=ft/dt;
u=0.0;
x=[0;0];
z=0.0;
y = Cd*x;
Yr=10;
for i=1:N
u = -Fd*x + Kd*z;
zn =z + ( Yr -y);
xn = Ad*x + Bd*u;
y = Cd*x;
x=xn;
z=zn;
timo(i)=i*dt;
yout1(i,1)=x(1);
end
figure(6);
subplot(2,1,1);
plot(timo,yout1);
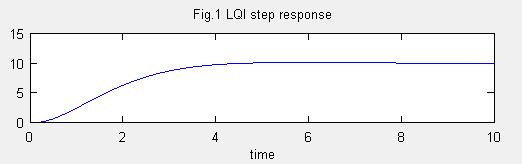
title('Fig.1 LQI step response')
xlabel('time');
 LQI
LQI
参考文献1のp74~を参考に
xo[i+1] = Axo[i] + Bu[i] + l*(y[i]-cxo[i])
l=
0.050644
0.019790
である。
%***********************************************
%1型最適サーボ + オブザーバー
%***********************************************
Ad = A
Bd = B
Cd = C
[n m]=size(Bd);
ABC=[Ad-eye(n) Bd;Cd zeros(m)];
FSD=[F*Ad F*Bd+eye(m)]*inv(ABC);
Fd=FSD(:,1:n)
Kd=FSD(:,n+1:m+n)
ft=10;
dt=0.1;
N=ft/dt;
%初期値
u=0.0;
xo=[0;0];%推定値 Observer
z=0.0;
x=[0;0];%実測
y=Cd*x;
Yr=10;%目標値
for i=1:N
u = -Fd*xo + Kd*z;
zn =z + ( Yr -y);
xno = Ad*xo+Bd*u+l*(y-Cd*xo);%Observer
xn=Ad*x+Bd*u;%制御対象モデル
x=xn;
xo=xno;
y=Cd*xn;%制御対象の出力
z=zn;
timoo(i)=i*dt;
youtt(i,1)=x(1);
end
figure(6);
subplot(2,1,2);
plot(timoo,youtt);
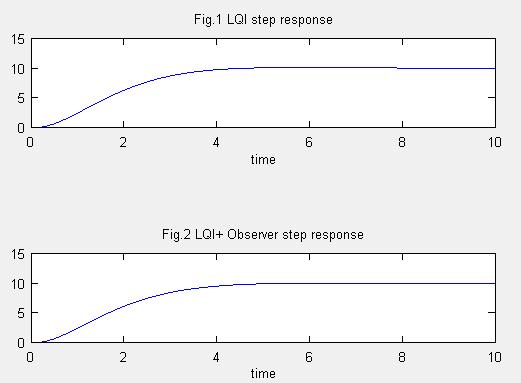
title('Fig.2 LQI+ Observer step response')
xlabel('time');
 LQI+Observer
LQI+Observer
clear;
max=201;
step=1/((max-1)/2);
in=zeros(1,max);
diff=zeros(1,max);
y=zeros(1,max);
x=-1:step:1;
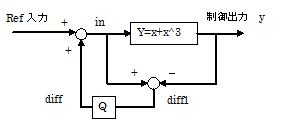
ref=sin(x*pi); #Reference入力(目標値)
y3=x+x.^3; #非線形制御対象
yout=ref+ref.^3; #オブザーバ無しの制御対象出力
for n=1:max
in(n)=ref(n)+diff(n);
y(n)=in(n)+in(n).^3;
diff1(n)=in(n)-y(n);
diff(n+1)=0.01*diff(n)+0.99*diff1(n);#Qフィルター
endfor
figure(1)
subplot(2,1,1)
plot(x,y3)
axis([-1 1 -2 2])
grid 'on'
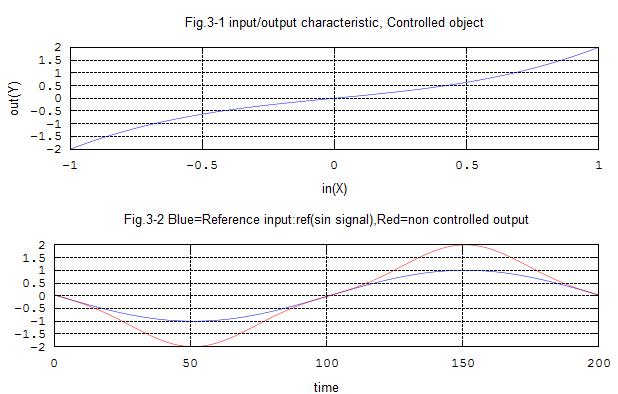
title('Fig.3-1 input/output characteristic, Controlled object')
xlabel('in(X)')
ylabel('out(Y)')
subplot(2,1,2)
n=1:1:max-1;
plot(n,ref(n),"b",n,yout(n),"r")
grid 'on'
title('Fig.3-2 Blue=Reference input:ref(sin signal),Red=non controlled output')
xlabel('time')
figure(2)
subplot(2,1,1)
n=1:1:max-1;
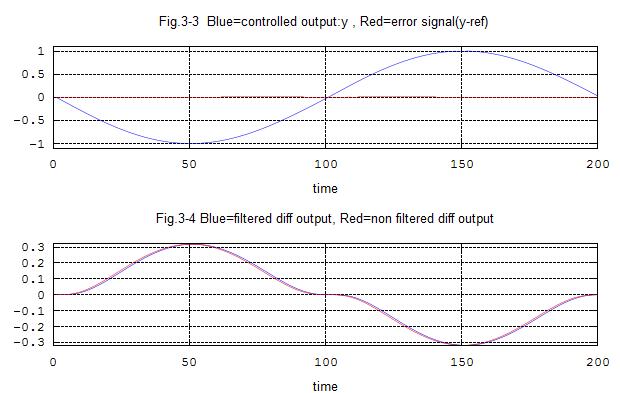
plot(n,y(n),"b",n,y(n)-ref(n),"r")
grid 'on'
title('Fig.3-3 Blue=controlled output:y , Red=error signal(y-ref) ')
xlabel('time')
subplot(2,1,2)
n=1:1:max-1;
plot(n,diff(n),"b",n,diff1(n),"r")
grid 'on'
title('Fig.3-4 Blue=filtered diff output, Red=non filtered diff output')
xlabel('time')